संख्याओं के साथ खेलना
NCERT Solutions
प्रश्नावली. 3.5
प्रश्न 1: निम्नलिखित में से कौन से कथन सत्य हैं?
- यदि कोई संख्या 3 से विभाज्य है, तो वह 9 से भी विभाजित होती है।
- यदि एक संख्या 9 से विभाज्य है, तो वह 3 से भी अवश्य विभाजित होगी।
- एक संख्या 18 से भी विभाज्य होती है, यदि वह 3 और 6 दोनों से विभाज्य हो।
- यदि एक संख्या 9 और 10 दोनों से विभाज्य हो, तो वह 90 से भी विभाजित होगी।
- यदि दो संख्याएँ सह-अभाज्य हों, तो उनमें से कम से कम एक अवश्य ही अभाज्य संख्या होगी।
- 4 से विभाज्य सभी संख्याएँ 8 से भी अवश्य विभाज्य होनी चाहिए।
- 8 से विभाज्य सभी संख्याएँ 4 से विभाज्य होनी चाहिए।
- यदि कोई संख्या दो संख्याओं को अलग-अलग पूरा-पूरा विभाजित करती है, तो वह उनके योग को भी पूरा-पूरा विभाजित करेगी।
- यदि कोई संख्या दो संख्याओं के योग को पूरी तरह विभाजित करती है, तो वह उन दोनों संख्याओं अलग-अलग भी विभाजित करेगी।
उत्तर: (a) असत्य (b) सत्य (c) सत्य (d) सत्य (e) असत्य (f) असत्य (g) सत्य (h) सत्य (i) असत्य
प्रश्न 2: यहाँ 60 के लिए दो भिन्न- भिन्न गुणनखंड वृक्ष दिए हैं। इनमें अज्ञात संख्याएँ लिखिए।
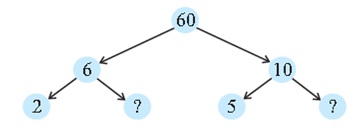
उत्तर: 3 और 2 (क्रमश:)
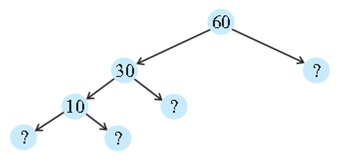
उत्तर: 2, 5, 3 और 2 (क्रमश:)
प्रश्न 3: एक भाज्य संख्या के अभाज्य गुणनखंडन में किन गुणनखंडो को सम्मिलित नहीं किया जाता है?
उत्तर: एक भाज्य संख्या के अभाज्य गुणनखंडन में 1 को सम्मिलित नहीं किया जाता है।
प्रश्न 4: चार अंकों की सबसे बड़ी संख्या लिखे और उसे अभाज्य गुणनखंडन के रूप में व्यक्त कीजिए।
उत्तर: चार अंकों की सबसे बड़ी संख्या = 9999
| 3 | 9999 |
| 3 | 3333 |
| 11 | 1111 |
| 101 |
इस प्रकार, 9999 का अभाज्य गुणनखंड है: 9999 = 3 × 3 × 11 × 101
प्रश्न 5: पांच अंकों की सबसे छोटी संख्या लिखे और उसे अभाज्य गुणनखंडन के रूप में व्यक्त कीजिए।
उत्तर: पांच अंकों की सबसे छोटी संख्या = 10000
| 2 | 10000 |
| 2 | 5000 |
| 2 | 2500 |
| 2 | 1250 |
| 5 | 625 |
| 5 | 125 |
| 5 | 25 |
| 5 | 5 |
| 1 |
इस प्रकार, 10000 का अभाज्य गुणनखंड है: 10000 = 2 × 2 × 2 × 2 × 5 × 5 × 5 × 5
प्रश्न 6: 1729 के सभी अभाज्य गुणनखंड ज्ञात कीजिए और उन्हें आरोही क्रम में व्यवस्थित कीजिए। अब दो क्रमागत अभाज्य गुणनखंडों में यदि कोई संबंध है तो लिखिए।
उत्तर:
| 7 | 1729 |
| 13 | 247 |
| 19 |
इस प्रकार, 9999 का अभाज्य गुणनखंड है: 1729 = 7 × 13 × 19 यही इसका आरोही क्रम भी है।
दो क्रमागत अभाज्य गुणनखंडो का अंतर 6 है।
प्रश्न 7: तीन क्रमागत संख्याओं का गुणनफल सदैव 6 से विभाज्य होता है। इस कथन को कुछ उदाहरणों की सहायता से स्पष्ट कीजिए।
उत्तर: तीन क्रमागत संख्याओं का गुणनफल जो सदैव 6 से विभाज्य होता है। उदाहरण:
2 × 3 × 4 = 24, ये 6 से विभाजित है।
5 × 6 × 7 = 210 ये 6 से विभाजित है।
प्रश्न 8: दो क्रमागत विषम संख्याओं का योग 4 से विभाज्य होता है। कुछ उदाहरण लेकर इस कथन का सत्यापन कीजिए।
उत्तर: दो क्रमागत विषम संख्याओं जिसका योग 4 से विभाज्य होता है। उदाहरण:
3 + 5 = 8, ये 4 से विभाजित है।
7 + 9 = 16 ये 6 से विभाजित है।
11 + 13 = 24 ये 6 से विभाजित है।
प्रश्न 9: निम्न में से किन व्यंजकों में अभाज्य गुणनखंडन किए गए है:
- 12 = 2 × 3 × 4
- 56 = 1 × 7 × 2 × 2 × 2
- 70 = 2 × 5 × 7
- 54 = 2 × 3 × 9
उत्तर: (b) और (c) व्यंजकों में अभाज्य गुणनखंडन किए गए हैं।
प्रश्न 10: बिना भाग किए ज्ञात कीजिए कि क्या 25110 संख्या 45 से विभाज्य है।
[ संकेत: 5 और 9 सह-अभाज्य संख्याएँ है। दी हुई संख्या की 5 और 9 से विभाज्यता की जाँच कीजिए।]
उत्तर: 45 का अभाज्य गुणनखंड = 5 × 9
विभाज्यता के नियम अनुसार, यदि कोई संख्या एक संख्या से विभाजित होती है, वह संख्या इस संख्या के प्रत्येक गुणनखंड से भी विभाजित होगी।
इसतरह, 25110 संख्या 5 से विभाजित होगी।
25110 संख्या 9 से भी विभाजित होगी।
और, 25110 संख्या 45 से भी विभाजित होगी।
प्रश्न 11: संख्या 18, 2 और 3 दोनों से विभाज्य है। यह 2 × 3 = 6 से भी विभाज्य है। इसी प्रकार, एक संख्या 4 और 6 दोनों से विभाज्य है। क्या हम कह सकते हैं कि वह संख्या 4 × 6 = 24 से भी विभाज्य होगी। यदि नहीं, तो अपने उत्तर की पुष्टि के लिए एक उदाहरण दीजिए।
उत्तर: कुछ संख्याएँ तो विभाज्य होगी, लेकिन कुछ नहीं होगी।
जैसे: 72, जो 4, 6 और 24 से विभाजित होगी।
लेकिन संख्या 36 ये 4 और 6 दोनों से तो विभाजित होगी परंतु 24 से विभाजित नहीं होगी।
प्रश्न 12: मैं चार भिन्न-भिन्न अभाज्य गुणनखंडों वाली सबसे छोटी संख्या हूँ। क्या आप मुझे ज्ञात कर सकते हैं?
उत्तर: सबसे छोटी चार अभाज्य गुणनखंडो वाली संख्या = 2 × 3 × 5 × 7 = 210