वृत्त
अभ्यास 10.4
प्रश्न 1: 5 सेमी तथा 3 सेमी त्रिज्या वाले दो वृत्त दो बिंदुओं पर प्रतिच्छेद करते हैं तथा उनके केंद्रों के बीच की दूरी 4 सेमी है। उभयनिष्ठ जीवा की लम्बाई ज्ञात कीजिए।

उत्तर: ΔAMO में AM2 `= OA^2 - OM^2`
या, `AM^2 = 5^2 - OM^2`
या, `AM^2 = 25 – OM^2` ……………(1)
ΔAMO’ में `AM^2 = OA’^2 - (4 – OM)^2`
`AM^2 = 3^2 - (4^2 + OM^2 - 8OM)`
`= 9 – 16 – OM^2 + 8OM` ………….(2)
समीकरण (1) और (2) से
`25 – OM^2 = 8OM – OM^2 - 7`
या, `8OM = 25 + 7 – OM^2 + OM^2`
या, `8OM = 32`
या, `OM = (32)/8 = 4` cm
इसका मतलब है O’M = 0
OM के मान का उपयोग करके हम AM का मान इस तरह निकाल सकते हैं।
`AM^2 = 25 – 4^2 = 25 – 16 = 9`
या, AM = 3 cm
इसलिए AB `=2xx3=6` cm
प्रश्न 2: यदि एक वृत्त की दो समान जीवाएँ वृत्त के अंदर प्रतिच्छेद करें, तो सिद्ध कीजिए कि एक जीवा के खंड दूसरी जीवा के संगत खंडों के बराबर हैं।
उत्तर: केंद्र O वाले वृत्त की जीवाएँ AB और CD बिंदु M पर काटती हैं
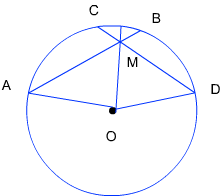
सिद्ध करना है: AM = DM और CM = BM
ΔAOM और ΔDOM में
OA = OD (त्रिज्या)
OM = OM (उभयनिष्ठ भुजा)
इसलिए, ΔAOM ≅ Δ DOM
इसलिए, AM = DM सिद्ध हुआ
दिया गया है AB = CD
इसलिए, AB – AM = CD – DM
या, CM = BM सिद्ध हुआ
प्रश्न 3: यदि एक वृत्त की दो समान जीवाएँ वृत्त के अंदर प्रतिच्छेद करें, तो सिद्ध कीजिए कि प्रतिच्छेद बिंदु को केंद्र से मिलाने वाली रेखा जीवाओं से बराबर कोण बनाती हैं।
उत्तर: इस प्रश्न को हल करने के लिए पिछले प्रश्न वाली आकृति का इस्तेमाल करते हैं।
सिद्ध करना है: ∠AMO = ∠DMO
ΔOMA और ΔOMD में
AO = OD (त्रिज्या)
OM = OM (उभयनिष्ठ)
इसलिए, ΔOMA ≅ ΔOMD
इसलिए, ∠AMO = ∠DMO सिद्ध हुआ
प्रश्न 4: यदि एक रेखा दो सकेंद्रीय वृत्तों को, जिनका केंद्र O है, A, B, C और D पर प्रतिच्छेद करे, तो सिद्ध कीजिए AB = CD है।

उत्तर:केंद्र O पर दो वृत्त बने हुए हैं। एक रेखा बड़े वृत्त को A और D बिंदुओं पर तथा छोटे वृत्त को B और C पर काटती है।
सिद्ध करना है: AB = CD
बड़े वृत्त की जीवा है AD
इसलिए, AM = MD ………..(1)
इसी तरह, छोटे वृत्त की जीवा BC है।
इसलिए, BM = MC …………(2)
समीकरण (1) और (2) से
AM – BM = MD – MC
या, AB = CD सिद्ध हुआ
प्रश्न 5: एक पार्क में बने 5 मी त्रिज्या वाले वृत्त पर खड़ी तीन लड़कियाँ रेशमा, सलमा एवं मनदीप खेल रही हैं। रेशमा एक गेंद को सलमा के पास, सलमा मनदीप के पास और मनदीप रेशमा के पास फेकती है। यदि रेश्मा और सलमा के बीच और सलमा तथा मनदीप के बीच की प्रत्येक दूरी 6 मी हो, तो रेशमा और मनदिप के बीच की दूरी क्या है?

उत्तर: केंद्र O पर एक वृत्त है। यहाँ, RS = SM = 6 m और त्रिज्या OS = 5 m
OS अब RM पर लम्ब OS खींचिए और SM पर लम्ब OL खींचिए।
ΔOMS में, आधार = OS और ऊँचाई = MN
Area (OMS) `= ½xx\MN\xx\OS= ½xx\MN\xx\5` ………….(1)
यदि आधार = SM = 6 m तो ऊँचाई = OL
क्षेत्रफल `=½xx\OL\xx\SM=½xx\OL\xx6` …………(2)
समीकरण (1) और (2) से
`5/2\MN= 3OL`
ΔOLM में,`OL^2 = OM^2 - ML^2`
`= 5^2 - 3^2`
`= 25 – 9 = 16`
या, `OL = 4`
इसलिए, `5/2\MN= 3xx4=12`
या, `MN=(24)/5=4.8`
इसलिए, `RM= 2xx4.8=9.6` m
प्रश्न 6: 20 मी त्रिज्या का एक गोल पार्क (वृत्ताकार) एक कालोनी मे स्थित है। तीन लड़के अंकुर, सैय्यद और डैविड इसकी परिसीमा पर बराबर दूरी पर बैठे हैं और प्रत्येक के हाथ में एक खिलौना टेलीफोन आपस में बात करने के लिए है। प्रत्येक फोन की डोरी की लंबाई ज्ञात कीजिए।

उत्तर: केंद्र O पर बना एक वृत्त है जिसकी त्रिज्या = 20 m और जीवाएँ AS = SD = AD = ?
ΔADS में `AM^2=AD^2-((AD)/2)^2`
या, `AM^2=AD^2-(AD^2)/4`
या, `AM^2=(3AD^2)/4`
या, `AM=(sqrt3)/2AD`
या, `AM=(sqrt3)/2AD=OM+20`
या, `OM = (sqrt3)/2AD -20` …………(1)
ΔODM में `OM^2=OD^2-((AD)/2)^2`
`= 20^2-(AD^2)/4`
`= 400–(AD^2)/4` ……………..(2)
समिकरण (1) और (2) से
`400– (AD^2)/4= ((sqrt3)/2AD-20)^2`
या, `400–(AD^2)/4=3/4xx\AD^2+400– 20sqrt3xx\AD`
या, ` (AD^2)/4=3/4xx\AD^2-20sqrt3AD`
या, `3/4 AD^2+( AD^2)/4=20 sqrt3AD`
या, `AD^2=20 sqrt3AD`
या, AD`=20 sqrt3` हर तार की लम्बाई