संख्या पद्धति

अभ्यास 1.1

प्रश्न 1: क्या शून्य एक परिमेय संख्या है? क्या आप इसे `p/q` के रूप में लिख सकते हैं, जहाँ p और q पूर्णांक हैं और q ≠ 0 है?

उत्तर: शून्य को `p/q` के रूप में लिख सकते हैं, जहाँ p और q पूर्णांक हैं और q ≠ 0 है। इसलिए शून्य एक परिमेय संख्य है।

`0/1`, `0/2`, `0/3`, आदि।

प्रश्न 2: 3 और 4 के बीच में छ: परिमेय संख्याएँ ज्ञात कीजिए।

उत्तर: 3 और 4 को 3/1 and 4/1 भी लिख सकते हैं।

हमें 3 और 4 के बीच छ: परिमेय संख्याएँ ज्ञात करनी हैं, इसलिए अंश और हर को 6 + 1 यानि 7 से गुणा करते हैं।

`3=3/1=(3xx7)/(1xx7)=21/7`  and

`4=4/1=(4xx7)/(1xx7)=28/7`

अब हम `21/7` और `28/7` के बीच की तीन परिमेय संख्याएँ ज्ञात करेंगे, जो नीचे दी गई हैं।

`(22/7),(23/7),(24/7),(25/7),(26/7)  (27/7)`

प्रश्न 3: `3/5` और `4/5` के बीच में पाँच परिमेय संख्याएँ ज्ञात कीजिए।

उत्तर: सबसे पहले हम अंश और हर को 5 + 1 यानि 6 से गुणा करेंगे।

`3/5=(3xx6)/(5xx6)=18/30` और `4/5=(4xx6)/(5xx6)=24/30`

अब हम `(18)/(30)` और `(24)/(30)` के बीच की पाँच परिमेय संख्याएँ ज्ञात करेंगे।

`(19/30),(20/30),(21/30),(22/30),(23/30)`

`=(19/3),((2xx10)/(3xx10)),((7xx3)/(10xx3))`,`((11xx2)/(15xx2)), (23/30)`

`=(19/30),(2/3),(7/10),(11/15)` और `(23/30)`

प्रश्न 4: नीचे दिए गए कथन सत्य हैं या असत्य? कारण के साथ अपने उत्तर दीजिए।

(a) प्रत्येक प्राकृत संख्या एक पूर्ण संख्या होती है।

उत्तर: गिनती के लिए प्रयोग में लाये जाने वाली संख्याओं को प्राकृत संख्या कहते हैं। इस समुच्च्य में यदि शून्य को शामिल कर लिया जाये तो तो इन्हें पूर्ण संख्या कहते हैं। इसलिए यह कथन सत्य है।

(b) प्रत्येक पूर्णांक एक पूर्ण संख्या होती है।

उत्तर: पूर्णांक ऋणात्मक और धनात्मक दोनों होते हैं लेकिन पूर्ण संख्याएँ केवल धनात्मक होती हैं। इसलिए यह कथन असत्य है।

(c) प्रत्येक परिमेय संख्या एक पूर्ण संख्या होती है।

उत्तर: परिमेय संख्या पूर्ण भी हो सकती है और नहीं भी हो सकती है। परिमेय संख्या ऋणात्मक भी हो सकती है। इसलिए यह कथन असत्य है।

अभ्यास 1.2

प्रश्न 1: नीचे दिए गए कथन सत्य हैं या असत्य हैं। कारण के साथ अपने उत्तर दीजिए।

(a) प्रत्येक अपरिमेय संख्या एक वास्तविक संख्या होती है।

उत्तर: जिस किसी भी संख्या के बारे में हम सोच सकते हैं उसे वास्तविक संख्या कहते हैं। हम अपरिमेय संख्या के बारे में भी सोच सकते हैं इसलिए प्रत्येक अपरिमेय संख्या एक वास्तविक संख्या होती है। इसलिए यह कथन सत्य है।

(b) संख्या रेखा का प्रत्येक बिंदु `sqrt\m` के रूप का होता है, जहाँ m एक प्राकृत संख्या है।

उत्तर: किसी भी संख्या का वर्गमूल ऋणात्मक नहीं हो सकता है। लेकिन संख्या रेखा पर ऋणात्मक संख्याएम भी होती हैं। इसलिए यह कथन असत्य है।

(c) प्रत्येक वास्तविक संख्या एक अपरिमेय संख्या होती है।

उत्तर: प्रत्येक अपरिमेय संख्या और परिमेय संख्या वास्तविक संख्या होती है। लेकिन इसका यह मतलब नहीं है कि प्रत्येक वास्तविक संख्या एक अपरिमेय संख्या होती है। इसलिए यह कथन असत्य है।

प्रश्न 2: क्या सभी धनात्मक पूर्णांकों के वर्गमूल अपरिमेय होते हैं? यदि नहीं, तो एक ऐसी संख्या के वर्गमूल का उदाहरण दीजिए जो एक परिमेय संख्या है।

उत्तर: ऐसी कई संख्याएँ हैं, जैसे 4, 16, 9, आदि।

प्रश्न 3: दिखाइए कि संख्या रेखा पर `sqrt5` को किस प्रकार निरूपित किया जा सकता है।

उत्तर: `sqrt5` को संख्या रेखा पर इस तरह दिखाया जा सकता है।

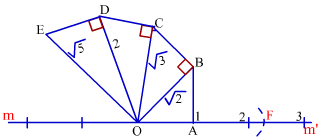
एक संख्या रेखा mm’ खींचिए।
इस रेखा पर 1 इंच या 1 इकाई का रेखाखंड OA लीजिए।
बिंदु A पर 1 इकाई का लम्ब AB खींचिए।
अब OB को मिलाइए। OB का मान √2 के बराबर होगा।
अब बिंदु B पर OB रेखाखंड 1 इकाई का लम्ब BC खींचिए।
अब OC को मिलाइए। OC का मान √3 के बराबर होगा।
अब OA के बराबर और OC के लम्बवत CD खींचिए।
अब OD को मिलाइए। इसका मान √4 यानि 2 के बराबर होगा।
अब OD के लम्बवत 1 इकाई की ED खींचिए।
अब OE को मिलाइए। इसका मान √5 के बराबर होगा।
अब संख्या रेखा पर OE के बराबर रेखाखंड OF खींचिए। इसका मान √5 होगा।
अब पता करते हैं कि कैसे OE का मान √5 के बराबर है।
यहाँ, OD = 2, DE = 1 और कोण ODE = 90º

पाइथागोरस प्रमेय के अनुसार,

`OE=sqrt(OD^2+DE^2)`
Or, `OE=sqrt(2^2+1^2)`
Or, `OE=sqrt(4+1)`
Or, `OE=sqrt5`