वृत्त

अभ्यास 10.2 Part 2

प्रश्न 4: सिद्ध कीजिए कि किसी वृत्त के किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समांतर होती हैं।

उत्तर: संरचना: एक वृत्त बनाईए जिसका केंद्र O है। व्यास AB खींचिए। अब स्पर्श रेखाएँ MN और OP खींचिए जो क्रमश: A और B को स्पर्श करती हैं।

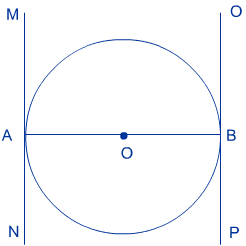
सिद्ध करना है: MN || OP

`∠MAB = ∠PBA = 90°` (स्पर्श रेखा पर त्रिज्या अभिलम्ब होता है।

चूँकि एकांतर कोण बराबर हैं

इसलिए; MN || OP सिद्ध हुआ।

प्रश्न 5: सिद्ध कीजिए कि स्पर्श बिंदु से स्पर्श रेखा पर खींचा गया लंब वृत्त के केंद्र से होकर जाता है।

उत्तर: एक वृत्त खींचिए जिसका केंद्र O है। स्पर्श रेखा AB खींचिए जो बिंदु P पर स्पर्श करती है।

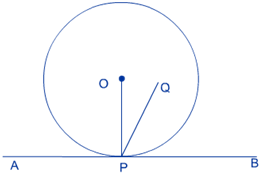
मान लीजिए कोई बिंदु O’ है जो बिंदु O का सन्निपाती नहीं है।

मान लीजिए कि AB पर PO’ अभिलम्ब है।

लेकिन AB पर PO लम्बवत होगा क्योंकि त्रिज्या हमेशा स्पर्श रेखा के लम्बवत होती है।

साथ में दी गई आकृति से ये भी पता चलता है कि ∠O’PB < ∠OPB

हमने जो पहले माना था उसके अनुसार इन कोणों को समकोण होना चाहिए।

लेकिन हमने ये भी माना था कि O और O’ सन्निपाती नहीं है। इसलिए दोनों कोण समकोण नहीं हो सकते हैं।

इसलिए यह सिद्ध हुआ कि स्पर्श रेखा पर स्पर्श बिंदु पर पड़ने वाला अभिलम्ब केंद्र से होकर जाता है।

प्रश्न 6: एक बिंदु A से, जो एक वृत्त के केंद्र से 5 सेमी दूरी पर है, वृत्त पर स्पर्श रेखा की लंबाई 4 सेमी है। वृत्त की त्रिज्या ज्ञात कीजिए।

उत्तर: यहाँ पर; OA = 5 cm, AB = 4 cm, OB = ?

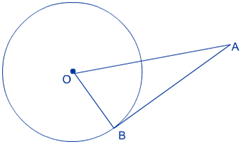
पाइथागोरस प्रमेय के अनुसार,

ΔOBA में

`OB^2 = OA^2 – BA^2`

`= 5^2 – 4^2`

`= 25 – 16 = 9`

या, `OB = 3` cm

प्रश्न 7: दो संकेंद्रीय वृत्तों की त्रिज्याएँ 5 सेमी तथा 3 सेमी हैं। बड़े वृत्त की उस जीवा की लंबाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती हो।

उत्तर: यहाँ पर; OA = 5 cm, OP = 3 cm, AB = ?

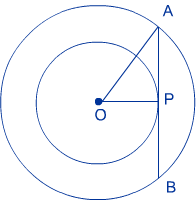
ΔOPA में,

`AP^2 = OA^2 – OP^2`

`= 5^2 – 3^2`

`= 25 – 9 = 16`

या, `AP = 4` cm

चूँकि AB को OP समद्विभाजित करता है

इसलिए, `AP = AB`

इसलिए, `AB = 2 xx 4 = 8` cm