ज्यामितीय संरचनाएँ

अभ्यास 11.1 Part 2

प्रश्न 4: आधार 8 सेमी तथा ऊँचाई 4 सेमी के एक समद्विबाहु त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ इस समद्विबाहु त्रिभुज की संगत भुजाओं की `1\1/2` गुनी हों।

उत्तर: त्रिभुज का निर्माण:

• एक रेखाखंड AB = 8 cm खींचिए।
• बिंदु A और B से AB के दोनों तरफ 4 सेमी की दूरी पर दो चाप खींचिए जो आपस में काटती हों।
• इन चापों कि मिलाइए ताकि AB का समद्विभाजक CD मिले। (चूँकि समद्विबाहु त्रिभुज में आधार का लम्बवत समद्विभाजक त्रिभुज की ऊँचाई के बराबर होता है)
• बिंदु A और B को C से मिलाने पर त्रिभुज ABC बनता है।

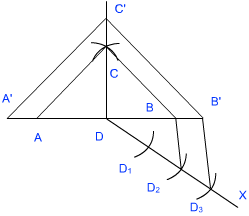
• बिंदु D से न्यूनकोण पर एक किरण DX खींचिए।
• अब DX पर तीन बिंदु बनाइए ताकि DD₁ = D₁D₂ = D₂D₃.
• बिंदु D₂ को बिंदु B से मिलाइए।
• बिंदु D₃ D₂B के समांतर एक रेखा खींचिए जो AB के बढ़ाए हुए भाग से बिंदु B’ पर मिलती हो।
• अब B’C’ || BC खींचिए।
• A’C’ || AC खींचिए।

इससे त्रिभुज A’B’C’ बनता है।

प्रश्न 5: एक त्रिभुज ABC बनाइए जिसमें BC = 6 सेमी, AB = 5 सेमी और ∠ABC = 60 हो। फिर एक त्रिभुज की रचना कीजिए जिसकी भुजाएँ ΔABC की संगत भुजाओं की `3/4` गुनी हों

उत्तर: त्रिभुज का निर्माण:

• एक रेखाखंड AB = 5 cm खींचिए।
• बिंदु B से एक 60^o कोण बनाइए और BC = 6 cm खींचिए।
• A को C से मिलाने पर त्रिभुज ABC बनता है।

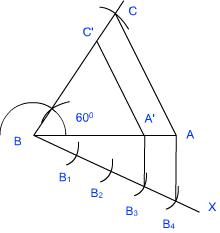
आधार का विभाजन:

• BA पर न्यूनकोण बनाती हुई एक किरण खींचिए।
• BA पर चार बिंदु बनाइए ताकि BB₁ = B₁B₂ = B₂B₃ = B₃3B₄.
• बिंदु B₄ बिंदु A से मिलाइए।
• बिंदु B₃ से B₄A के समांतर रेखा खींचिए जो AB से बिंदु A’ पर मिलती है।
• A’C’ || AC खींचिए।

इससे त्रिभुज A’C’B बनता है

प्रश्न 6: एक त्रिभुज ABC बनाइए, जिसमें BC = 7 सेमी, ∠B = 45°, ∠A = 105° हो। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ΔABC की संगत भुजाओं की `4/3` गुनी हों।

उत्तर: त्रिभुज का निर्माण:

• एक रेखाखंड BC = 7 cm खींचिए।
• बिंदु B पर 45^o कोण बनाइए और बिंदु C पर 30^o का कोण बनाइए (क्योंकि 45 + 30 + 105 = 180).
• बिंदु B और C को बिंदु A से मिलाइए
• इससे त्रिभुज ABC बनता है।

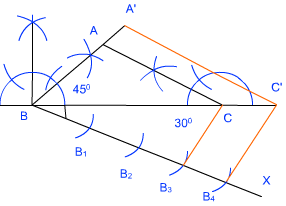
आधार का विभाजन:

• एक किरण BX खींचिए जो बिंदु B से न्यूनकोण बनाती हो।
• अब BX पर चार बिंदु डालिए ताकि BB₁ = B₁B₂ = B₂B₃ = B₃B₄.
• अब B₃ को C से मिलाइए।
• बिंदु B₄ से B₃C के समांतर एक रेखा खींचिए जो BC से बिंदु C’ पर मिलती हो।
• A’C’ || AC खींचिए।

इससे त्रिभुज A’BC’ बनता है।

प्रश्न 7: एक समकोण त्रिभुज की रचना कीजिए, जिसकी भुजाएँ (कर्ण के अतिरिक्त) 4 सेमी तथा 3 सेमी लंबाई की हों। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की `5/3` गुनी हों।

उत्तर: त्रिभुज का निर्माण:

एक रेखाखंड AB = 3 cm खींचिए

बिंदु A पर एक समकोण बनाइए और इस बिंदु से AC = 4 खींचिए।

A और B को मिलाने से त्रिभुज ABC बनता है।

आधार का विभाजन:

• एक किरण AX खींचिए जो AB के साथ न्यूनकोण बनाती है।
• AX पर पाँच बिंदु बनाइए ताकि AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅.
• Join A₃ to point B.
• बिंदु A₅ से A₃B के समांतर एक रेखा खींचिए जो AB से बिंदु B’ पर मिलती है।
• C’B’ || CB खींचिए।

इससे त्रिभुज A’B’C’ बनता है।