त्रिभुज के गुण
अभ्यास 6.3
प्रश्न 1: निम्नाकित आकृतियों में अज्ञात x का मान ज्ञात कीजिए।
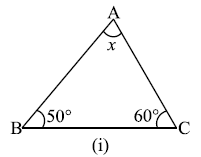
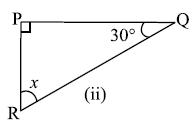
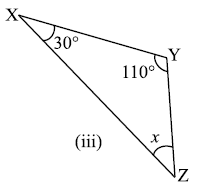
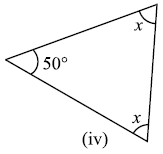
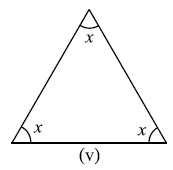
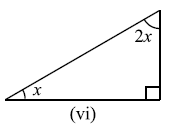
उत्तर: (i) 70°, (ii) 60°, (iii) 40°, (iv) 65°, (v) 60°, (vi) 30°
प्रश्न 2: निम्नाकित आकृतियों में अज्ञात x और y का मान ज्ञात कीजिए।
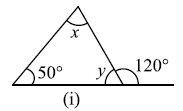
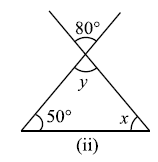
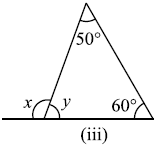
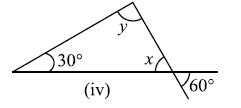
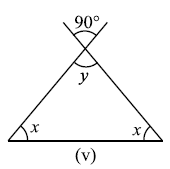
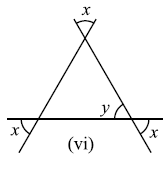
उत्तर: (i) `x=70°`, `y=60°`, (ii) `x=50°`, `y=80°`, (iii) `x=110°`, `y=70°, (iv) `x=60°`, `y=90°`, (v) `x=45°`, `y=90°`, (vi) `x=y=60°`
अभ्यास 6.4
प्रश्न 1: निम्न दी हुई भुजाओं की मापों से क्या कोई त्रिभुज संभव है?
(i) 2 cm, 3 cm 5 cm (ii) 3 cm, 6 cm, 7 cm (iii) 6 cm, 3 cm, 2 cm
उत्तर: केवल दूसरे विकल्प में दी भुजाओं से त्रिभुज संभव है। किसी भी दो भुजाओं का योग तीसरी भुजा से अधिक है।
प्रश्न 2: त्रिभुज PQR के अभ्यंतर में कोई बिंदु O लीजिए। क्या यह सही है कि
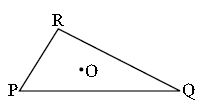
- OP + OQ > PQ?
- OQ + OR > QR?
- OR + OP > RP?
उत्तर: तीनों विकल्पों में दी गई भुजाएँ त्रिभुज की भुजाएँ हैं। त्रिभुज की किसी भी दो भुजाओं का योग तीसरी भुजा से अधिक होता है। इसलिए तीनों विकल्प सही हैं।
प्रश्न 3: त्रिभुज ABC की एक माध्यिका AM है। बताइए कि क्या AB + BC + CA > 2 AM?
(संकेत: त्रिभुज ABM तथा त्रिभुज AMC की भुजाओं पर विचार कीजिए।)
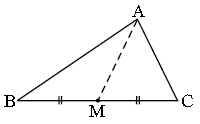
उत्तर: ΔABM में,
AB + BM &get; AM
ΔAMC में,
AC + MC > AM
दोनों समीकरणों को जोड़ने पर
AB + BM + MC + AC > AM + AM
या, AB + BC + AC > 2AM
प्रश्न 4: ABCD एक चतुर्भुज है। क्या AB + BC + CD + DA > AC + BD?
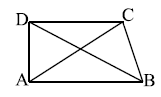
उत्तर: ΔABC
AB + BC > AC
ΔADC
AD + DC > AC
ΔDAB
DA + AB > DB
ΔDCB
DC + BC > DB
AB + BC + AD + DC + DA + AB + DC + BC > 2(AC + DB)
2(AB + BC + CD + AD) > 2(AC + DB)
AB + BC + CD + AD > AC + BD
प्रश्न 5: ABCD एक चतुर्भुज है। क्या AB + BC + CD + DA < 2(AC + BD)?
उत्तर: पिछले प्रश्न से,
2(AB + BC + CD + AD) > 2(AC + DB)
AB + BC + CD + AD > AC + BD
दोनों समीकरणों से यह सिद्ध होता है कि
AB + BC + CD + DA < 2(AC + BD)
प्रश्न 6: एक त्रिभुज की दो भुजाओं की माप 12cm तथा 15cm है। इसकी तीसरी भुजा की माप किन दो मापों के बीच होनी चाहिए?
उत्तर: 12 + 15 = 27
इसलिए तीसरी भुजा की माप 27 सेमी से कम होनी चाहिए
12 में कम से कम 4 जोड़ने से योगफल 15 से अधिक होता है। इसलिए तीसरी भुजा की माप 4 से लेकर 26 तक कोई भी संख्या हो सकती है।