हीरोन फॉर्मूला

अभ्यास 12.2

Part 2

प्रश्न 5: एक समचतुर्भुजाकार घास के खेत में 18 गायों के चरने के लिए घास है। यदि इस समचतुर्भुज की प्रत्येक भुजा 30 मी है और बड़ा विकर्ण 48 मी है, तो प्रत्येक गाय को चरने के लिए इस घास के खेत का कितना क्षेत्रफल प्राप्त होगा।

उत्तर: दिया गया है; AB = BC = CD = AD = 30 cm और AC = 48 m

इसलिए, AO = 24 m

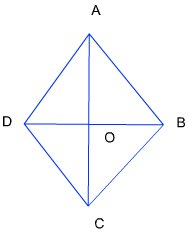
ΔAOB में: `BO^2=AB^2-AO^2`

`=30^2-24^2`

`=900–576=324`

या, `BO=18` m

इसलिए समचतुर्भुज का दूसरा विकर्ण `=18xx2=36` m

समचतुर्भुज का क्षेत्रफल `=1/2xxd_1xx\d_2`

`=1/2xx48xx36=864` sq m

इसलिए प्रति गाय क्षेत्रफल `=(864)/(18)=48` sq m

प्रश्न 6: दो विभिन्न रंगों के कपड़ों के 10 त्रिभुजाकार टुकड़ों को सीकर एक छाता बनाया गया है। प्रत्येक टुकड़े के माप 20 सेमी, 50 सेमी और 50 सेमी है। छाते में प्रत्येक रंग का कितना कपड़ा लगा है?

उत्तर: a = 20 cm, b = 50 cm, c= 50 cm

इसलिए, `s=(20+50+50)/2 = 60`

क्षेत्रफल `=sqrt(s(s-a)(s-b)(s-c))`

`=sqrt(60(60-50)(60-50)(60-20))`

`=sqrt(60xx10xx10xx40)`

`=sqrt(10^4xx2^2xx6)=200sqrt6` sq cm

हर रंग के कपड़े का क्षेत्रफल `=10xx200sqrt6` sq cm

प्रश्न 7: एक पतंग तीन भिन्न-भिन्न शेडों के कागजों से बनी है। इन्हें इस आकृति में I, II और III से दिखाया गया है। पतंग का ऊपरी भाग 32 सेमी विकर्ण का एक वर्ग है और निचला भाग 6 सेमी, 6 सेमी और 8 सेमी भुजाओं का एक समद्विबाहु त्रिभुज है।ज्ञात कीजिए कि प्रत्येक शेड का कितना कागज प्रयुक्त किया गया है।

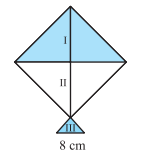
उत्तर: वर्ग का क्षेत्रफल `=1/2xx32xx32=512` sq cm

(जब विकर्ण दिये हुए हों तो वर्ग का क्षेत्रफल वैसे ही निकाला जा सकता है, जैसे समचतुर्भुज का क्षेत्रफल निकालते हैं)

इसलिए आकृति I का क्षेत्रफल = shape II

`=(512)/2=256` sq cm

अब त्रिभुजाकार आकृति के लिए: a = 6 cm, b = 6 cm और c = 8 cm

इस आकृति के लिए `s=(6+6+8)/2=10`

क्षेत्रफल `=sqrt(s(s-a)(s-b)(s-c))`

`=sqrt(10(10-6)(10-6)(10-8))`

`=sqrt(10xx4xx4xx2)=8sqrt5` sq cm

प्रश्न 8: फर्श पर एक फूलों का डिजाइन 16 त्रिभुजाकार टाइलों से बनाया गया है, जिनमें से प्रत्येक की भुजाएँ 9 सेमी, 28 सेमी और 35 सेमी हैं। इन टाइलों को 50 पैसे प्रति वर्ग सेमी की दर से पॉलिश कराने का व्यय ज्ञात कीजिए।

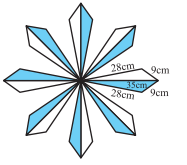
उत्तर:दिया गया है, a = 9 cm, b = 28 cm और c = 35 cm

इसलिए, `s=(9+28+35)/2=36`

क्षेत्रफल `=sqrt(s(s-a)(s-b)(s-c))`

`=sqrt(36(36-35)(36-28)(36-9))`

`=sqrt(36xx1xx8xx27)`

`=sqrt(6^2xx2^2xx3^2xx6)=36sqrt6` sq cm

खर्च `=16xx36sqrt6xx0.50 = Rs. 288sqrt6`

प्रश्न 9: एक खेत समलंब के आकार का है जिसकी समांतर भुजाएँ 25 मी और 10 मी हैं। इसकी असमांतर भुजाएँ 14 मी और 13 मी हैं। इस खेत का क्षेत्रफल ज्ञात कीजिए।

उत्तर: ABCD एक समलंब है जिसमें AB = 10 cm, DC – 25 cm, BC = 14 cm और AD = 13 cm

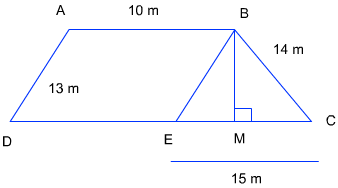
BE||AD खींचिए

ΔBEC में, a = 13 cm, b = 14 cm और c = 15 cm

इसलिए, `s=(13 + 14 + 15)/2=21`

क्षेत्रफल `=sqrt(s(s-a)(s-b)(s-c))`

`=sqrt(21(21-13)(21-14)(21-15))`

`=sqrt(21xx8xx7xx6)`

`=sqrt(7xx2xx2xx2xx2xx7xx3)=84` sq cm

अब ऊँचाई BM का मान इस तरह निकाल सकते हैं

त्रिभुज का क्षेत्रफल `=1/2xx\Ba\se\xx\He\ig\ht`

`= 1/2xx\EC\xx \BM`

या, `84=1/2xx15xx\BM`

या, `BM= (84xx2)/15=11.2` m

समलम्ब का क्षेत्रफल `=½xx` ऊँचाई `xx` (समांतर भुजाओं का योग)

`=½xx11.2xx(10+25)=5.6xx35=196` sq m